The Hypercube allows us to explore shadows of a \(4\)-cube under rotations about coordinate planes in \(4\)-space. The image below is a screenshot. Please visit the link for the live software.
About the Math (tl; dr): In four-space with rectangular coordinates \((x_{1}, x_{2}, x_{3}, x_{4})\), there are six coordinate planes in which we can rotate. Identify \(3\)-space with the set \((x_{1}, x_{2}, x_{3}, 0)\). Rotating in a coordinate plane contained in \(3\)-space corresponds to an ordinary spatial rotation. Rotating in any of the three coordinate planes containing the \(x_{4}\)-axis does not.
Instructions: Three pairs of keys effect rotation in the three coordinate planes containing the \(x_{4}\)-axis. Greater-than and less-than move the viewpoint closer or farther from the cube.
Viewpoint: The \(4\)-cube can be rotated in space using the arrow keys. Up and Down control pitch (tilt), while Left and Right control yaw (pan).
About the Math in more detail: If we construe a rotation as having an axis—a line that does not move, we erroneously fixate on a special feature of \(3\)-space. In a more accurate conceptual approximation, a rotation moves a plane and fixes everything perpendicular to that plane.
This description correctly describes rotations in \(2\)-space (a plane, where rotations fix one point) and \(3\)-space (where rotations fix a line). Perhaps counter-intuitively, however, this description over-simplifies the situation in \(4\)-space, where mutually-orthogonal planes exist. In rectangular coordinates \((x_{1}, x_{2}, x_{3}, x_{4})\), for example, the set of points \((x_{1}, x_{2}, 0, 0)\) is a plane, and the set of points \((0, 0, x_{3}, x_{4})\) is a plane. These planes intersect in a single point, \((0, 0, 0, 0)\), and are as perpendicular to each other as two coordinate axes. We can rotate each plane through an arbitrary angle, obtaining a rotation of \(4\)-space that generally fixes only the origin. (Even this is not everything: We need not have picked coordinate planes at all, much less this particular pair. And in dimensions greater than four, there might exist more than two mutually-perpendicular planes. Those considerations are beyond the scope of this post, but do suggest why rotations differ in even-dimensional spaces compared to odd-dimensional spaces.)
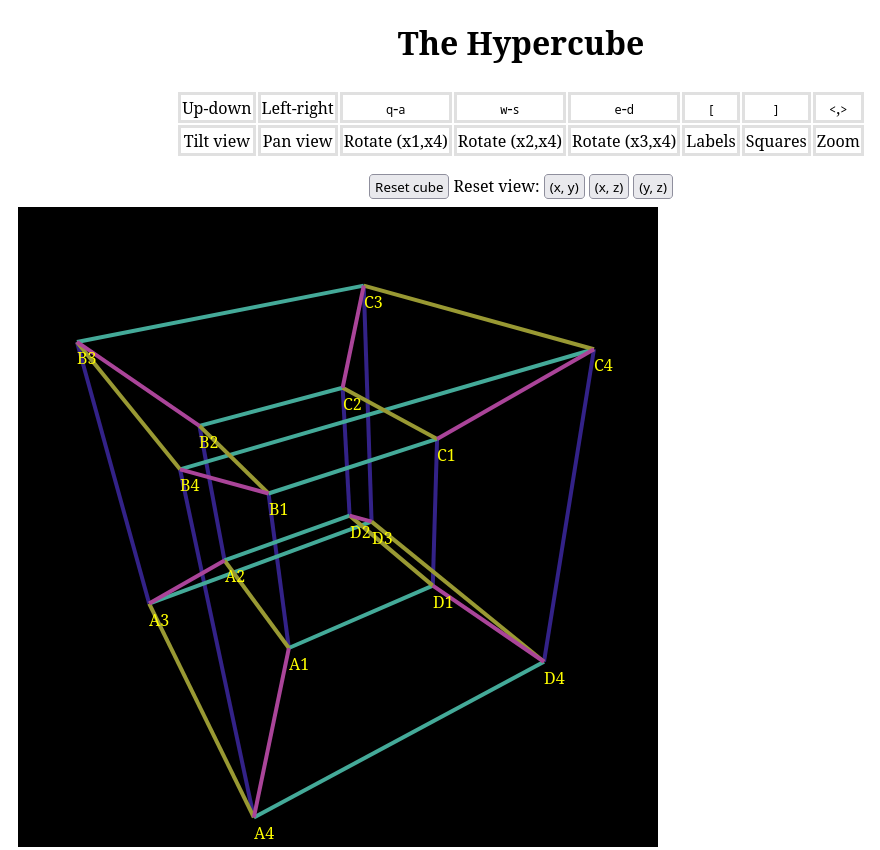
The ordered product \([-1, 1]^{2} = [-1, 1] \times [-1, 1]\), comprising points whose rectangular coordinates are between \(-1\) and \(1\) inclusive, is a square in a plane. Put one copy of this square in the \((x_{1}, x_{2}, 0, 0)\) plane with vertices labeled \(\{A, B, C, D\}\). Put a second copy of this square in the \((0, 0, x_{3}, x_{4})\) plane with vertices labeled \(\{1, 2, 3, 4\}\). The right square bracket key toggles highlighting of these component squares. The ordered product of these squares is the entire \(4\)-cube, whose \(16\) vertices are labeled \(A1\) through \(D4\).
A cube in arbitrary dimension \(n\) can be decomposed into \(k\)-dimensional faces. One pleasant way to count these is to decompose the closed interval \([-1, 1]\) into endpoints and interior: \(\{-1\} \cup (-1, 1) \cup \{1\}\). If \(1\) connotes an endpoint (a.k.a., \(0\)-dimensional face) and \(x\) connotes an interior (\(1\)-dimensional face), then the interval is represented by the monomial \(2 + x\): two endpoints and one interval. The key insight is, taking powers of this monomial algebraically represents the ordered product! Precisely, the coefficient of \(x^{k}\) in \((2 + x)^{n}\) is the number of \(k\)-dimensional faces in the \(n\)-cube. Thus \[ (2 + x)^{2} = 4 + 4x + x^{2} \] tells us a square has \(4\) vertices (the constant coefficient), \(4\) edges (the linear coefficient), and one square (the quadratic coefficient). Similarly, \[ (2 + x)^{3} = 8 + 12x + 6x^{2} + x^{3} \] counts the vertices, edges, square faces, and solid face of a \(3\)-cube. Since \[ (2 + x)^{4} = 16 + 32x + 24x^{2} + 8x^{3} + x^{4}, \] we conclude in particular that the \(4\)-cube has \(32\) edges. These are color-coded, and eight lie parallel to each coordinate axis. If edges of a single color do not appear parallel, that is merely an artifact of projection.